這篇文章是擼主要介紹人臉識別經典方法的第一篇，后續會有其他方法更新。特征臉方法基本是將人臉識別推向真正可用的第一種方法，了解一下還是很有必要的。特征臉用到的理論基礎PCA在另一篇博客里：特征臉(Eigenface)理論基礎-PCA(主成分分析法) 。本文的參考資料附在最后了^_^

步驟一：獲取包含M張人臉圖像的集合S。在我們的例子里有25張人臉圖像（雖然是25個不同人的人臉的圖像，但是看著怎么不像呢，難道我有臉盲癥么），如下圖所示哦。每張圖像可以轉換成一個N維的向量（是的，沒錯，一個像素一個像素的排成一行就好了，至于是橫著還是豎著獲取原圖像的像素，隨你自己，只要前后統一就可以），然后把這M個向量放到一個集合S里，如下式所示。

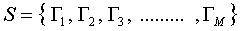
步驟二：在獲取到人臉向量集合S后，計算得到平均圖像Ψ，至于怎么計算平均圖像，公式在下面。就是把集合S里面的向量遍歷一遍進行累加，然后取平均值。得到的這個Ψ其實還挺有意思的，Ψ其實也是一個N維向量，如果再把它還原回圖像的形式的話，可以得到如下的“平均臉”，是的沒錯，還他媽的挺帥啊。那如果你想看一下某計算機學院男生平均下來都長得什么樣子，用上面的方法就可以了。

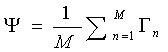
步驟三：計算每張圖像和平均圖像的差值Φ，就是用S集合里的每個元素減去步驟二中的平均值。

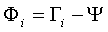
步驟四：找到M個正交的單位向量un，這些單位向量其實是用來描述Φ（步驟三中的差值）分布的。un里面的第k（k=1,2,3...M)個向量uk是通過下式計算的，

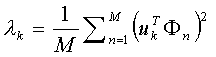
當這個λk（原文里取了個名字叫特征值）取最小的值時，uk基本就確定了。補充一下，剛才也說了，這M個向量是相互正交而且是單位長度的，所以啦，uk還要滿足下式：

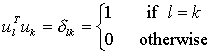
上面的等式使得uk為單位正交向量。計算上面的uk其實就是計算如下協方差矩陣的特征向量：

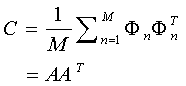
其中

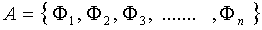
對于一個NxN（比如100x100）維的圖像來說，上述直接計算其特征向量計算量實在是太大了（協方差矩陣可以達到10000x10000），所以有了如下的簡單計算。