一、簡介
平衡二叉樹(BalancedBinary Tree或Height-Balanced Tree)
又稱AVL樹。它或者是一棵空樹,或者是具有下列性質(zhì)的二叉樹:它的左子樹和右子樹都是平衡二叉樹,且左子樹和右子樹的深度之差的絕對值不超過1。若將二叉樹上結(jié)點的平衡因子BF(BalanceFactor)定義為該結(jié)點的左子樹的深度減去它的右子樹的深度,則平衡二叉樹上所有結(jié)點的平衡因子只可能是-1、0和1。(此段定義來自嚴蔚敏的《數(shù)據(jù)結(jié)構(gòu)(C語言版)》)
紅黑樹
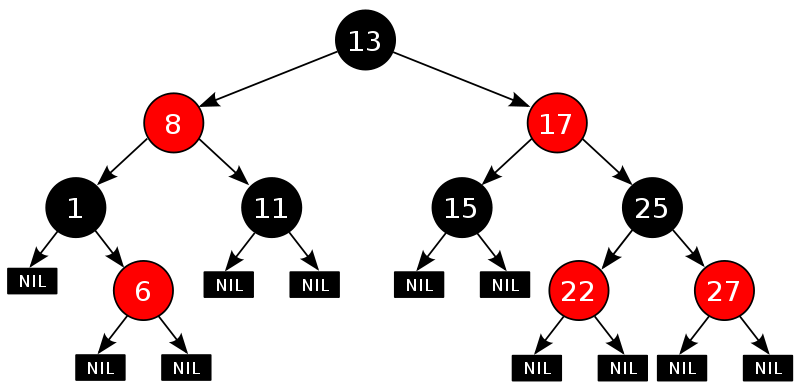
R-B Tree,全稱是Red-Black Tree,又稱為“紅黑樹”,它一種特殊的二叉查找樹。紅黑樹的每個節(jié)點上都有存儲位表示節(jié)點的顏色,可以是紅(Red)或黑(Black)。
紅黑樹是一種在插入或刪除結(jié)點時都需要維持平衡的二叉查找樹,并且每個結(jié)點都具有顏色屬性:
(1)、一個結(jié)點要么是紅色的,要么是黑色的。
(2)、根結(jié)點是黑色的。
(3)、如果一個結(jié)點是紅色的,那么它的子結(jié)點必須是黑色的,也就是說在沿著從根結(jié)點出發(fā)的任何路徑上都不會出現(xiàn)兩個連續(xù)的紅色結(jié)點。
(4)、從一個結(jié)點到一個NULL指針的每條路徑上必須包含相同數(shù)目的黑色結(jié)點。
Linux內(nèi)核紅黑樹的算法都定義在linux-2.6.38.8/include/linux/rbtree.h和linux-2.6.38.8/lib/rbtree.c兩個文件中。
二、結(jié)構(gòu)體
struct rb_node { unsigned long rb_parent_color; #define RB_RED 0 #define RB_BLACK 1 struct rb_node *rb_right; struct rb_node *rb_left; } __attribute__((aligned(sizeof(long)))); 這里的巧妙之處是使用成員rb_parent_color同時存儲兩種數(shù)據(jù),一是其雙親結(jié)點的地址,另一是此結(jié)點的著色。 __attribute__((aligned(sizeof(long))))屬性保證了紅黑樹中的每個結(jié)點的首地址都是32位對齊的(在32位機上),也就是說每個結(jié)點首地址的bit[1]和bit[0]都是0,因此就可以使用bit[0]來存儲結(jié)點的顏色屬性而不干擾到其雙親結(jié)點首地址的存儲。
操作rb_parent_color的函數(shù):
#define rb_parent(r) ((struct rb_node *)((r)->rb_parent_color & ~3)) //獲得其雙親結(jié)點的首地址 #define rb_color(r) ((r)->rb_parent_color & 1) //獲得顏色屬性 #define rb_is_red(r) (!rb_color(r)) //判斷顏色屬性是否為紅 #define rb_is_black(r) rb_color(r) //判斷顏色屬性是否為黑 #define rb_set_red(r) do { (r)->rb_parent_color &= ~1; } while (0) //設(shè)置紅色屬性 #define rb_set_black(r) do { (r)->rb_parent_color |= 1; } while (0) //設(shè)置黑色屬性 static inline void rb_set_parent(struct rb_node *rb, struct rb_node *p) //設(shè)置其雙親結(jié)點首地址的函數(shù) { rb->rb_parent_color = (rb->rb_parent_color & 3) | (unsigned long)p; } static inline void rb_set_color(struct rb_node *rb, int color) //設(shè)置結(jié)點顏色屬性的函數(shù) { rb->rb_parent_color = (rb->rb_parent_color & ~1) | color; } 初始化新結(jié)點:
static inline void rb_link_node(struct rb_node * node, struct rb_node * parent, struct rb_node ** rb_link) { node->rb_parent_color = (unsigned long )parent; //設(shè)置其雙親結(jié)點的首地址(根結(jié)點的雙親結(jié)點為NULL),且顏色屬性設(shè)為黑色 node->rb_left = node->rb_right = NULL; //初始化新結(jié)點的左右子樹 *rb_link = node; //指向新結(jié)點 } 指向紅黑樹根結(jié)點的指針:
struct rb_root { struct rb_node *rb_node; }; #define RB_ROOT (struct rb_root) { NULL, } //初始化指向紅黑樹根結(jié)點的指針 #define rb_entry(ptr, type, member) container_of(ptr, type, member) //用來獲得包含struct rb_node的結(jié)構(gòu)體的首地址 #define RB_EMPTY_ROOT(root) ((root)->rb_node == NULL) //判斷樹是否為空 #define RB_EMPTY_NODE(node) (rb_parent(node) == node) //判斷node的雙親結(jié)點是否為自身 #define RB_CLEAR_NODE(node) (rb_set_parent(node, node)) //設(shè)置雙親結(jié)點為自身 三、插入
首先像二叉查找樹一樣插入一個新結(jié)點,然后根據(jù)情況作出相應(yīng)的調(diào)整,以使其滿足紅黑樹的顏色屬性(其實質(zhì)是維持紅黑樹的平衡)。
函數(shù)rb_insert_color使用while循環(huán)不斷地判斷雙親結(jié)點是否存在,且顏色屬性為紅色。
若判斷條件為真,則分成兩部分執(zhí)行后續(xù)的操作:
(1)、當雙親結(jié)點是祖父結(jié)點左子樹的根時,則:
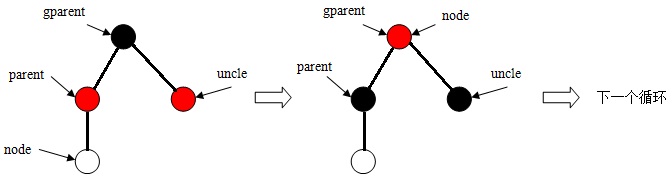
a、存在叔父結(jié)點,且顏色屬性為紅色。
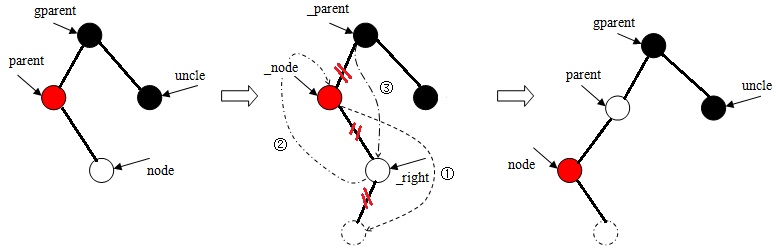
b、當node是其雙親結(jié)點右子樹的根時,則左旋,然后執(zhí)行第c步。
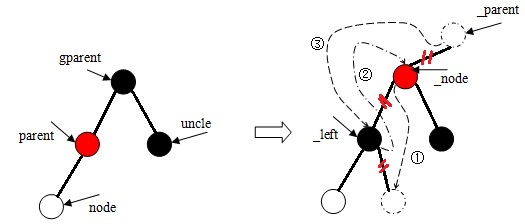
c、當node是其雙親結(jié)點左子樹的根時。
(2)、當雙親結(jié)點是祖父結(jié)點右子樹的根時的操作與第(1)步大致相同,這里略過不談。
若為假,則始終設(shè)置根結(jié)點的顏色屬性為黑色。
void rb_insert_color(struct rb_node *node, struct rb_root *root) { struct rb_node *parent, *gparent; while ((parent = rb_parent(node)) && rb_is_red(parent)) //雙親結(jié)點不為NULL,且顏色屬性為紅色 { gparent = rb_parent(parent); //獲得祖父結(jié)點 if (parent == gparent->rb_left) //雙親結(jié)點是祖父結(jié)點左子樹的根 { { register struct rb_node *uncle = gparent->rb_right; //獲得叔父結(jié)點 if (uncle && rb_is_red(uncle)) //叔父結(jié)點存在,且顏色屬性為紅色 { rb_set_black(uncle); //設(shè)置叔父結(jié)點為黑色 rb_set_black(parent); //設(shè)置雙親結(jié)點為黑色 rb_set_red(gparent); //設(shè)置祖父結(jié)點為紅色 node = gparent; //node指向祖父結(jié)點 continue; //繼續(xù)下一個while循環(huán) } } if (parent->rb_right == node) //當node是其雙親結(jié)點右子樹的根時 { register struct rb_node *tmp; __rb_rotate_left(parent, root); //左旋 tmp = parent; //調(diào)整parent和node指針的指向 parent = node; node = tmp; } rb_set_black(parent); //設(shè)置雙親結(jié)點為黑色 rb_set_red(gparent); //設(shè)置祖父結(jié)點為紅色 __rb_rotate_right(gparent, root); //右旋 } else { // !(parent == gparent->rb_left) { register struct rb_node *uncle = gparent->rb_left; if (uncle && rb_is_red(uncle)) { rb_set_black(uncle); rb_set_black(parent); rb_set_red(gparent); node = gparent; continue; } } if (parent->rb_left == node) { register struct rb_node *tmp; __rb_rotate_right(parent, root); tmp = parent; parent = node; node = tmp; } rb_set_black(parent); rb_set_red(gparent); __rb_rotate_left(gparent, root); } //end if (parent == gparent->rb_left) } //end while ((parent = rb_parent(node)) && rb_is_red(parent)) rb_set_black(root->rb_node); } 四、刪除
像二叉查找樹的刪除操作一樣,首先需要找到所需刪除的結(jié)點,然后根據(jù)該結(jié)點左右子樹的有無分為三種情形:
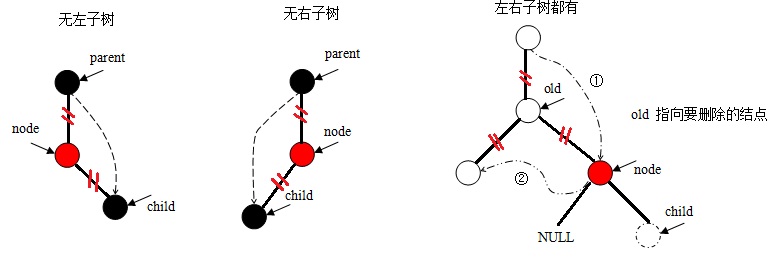
若node結(jié)點的顏色屬性為黑色,則需要調(diào)用__rb_erase_color函數(shù)來進行調(diào)整。
void rb_erase(struct rb_node *node, struct rb_root *root) { struct rb_node *child, *parent; int color; if (!node->rb_left) //刪除結(jié)點無左子樹 child = node->rb_right; else if (!node->rb_right) //刪除結(jié)點無右子樹 child = node->rb_left; else //左右子樹都有 { struct rb_node *old = node, *left; node = node->rb_right; while ((left = node->rb_left) != NULL) node = left; if (rb_parent(old)) { if (rb_parent(old)->rb_left == old) rb_parent(old)->rb_left = node; else rb_parent(old)->rb_right = node; } else root->rb_node = node; child = node->rb_right; parent = rb_parent(node); color = rb_color(node); if (parent == old) { parent = node; } else { if (child) rb_set_parent(child, parent); parent->rb_left = child; node->rb_right = old->rb_right; rb_set_parent(old->rb_right, node); } node->rb_parent_color = old->rb_parent_color; node->rb_left = old->rb_left; rb_set_parent(old->rb_left, node); goto color; } //end else parent = rb_parent(node); //獲得刪除結(jié)點的雙親結(jié)點 color = rb_color(node); //獲取刪除結(jié)點的顏色屬性 if (child) rb_set_parent(child, parent); if (parent) { if (parent->rb_left == node) parent->rb_left = child; else parent->rb_right = child; } else root->rb_node = child; color: if (color == RB_BLACK) //如果刪除結(jié)點的顏色屬性為黑色,則需調(diào)用__rb_erase_color函數(shù)來進行調(diào)整 __rb_erase_color(child, parent, root); } 五、遍歷
rb_first和rb_next函數(shù)可組成中序遍歷,即以升序遍歷紅黑樹中的所有結(jié)點。
struct rb_node *rb_first(const struct rb_root *root) { struct rb_node *n; n = root->rb_node; if (!n) return NULL; while (n->rb_left) n = n->rb_left; return n; } struct rb_node *rb_next(const struct rb_node *node) { struct rb_node *parent; if (rb_parent(node) == node) return NULL; /* If we have a right-hand child, go down and then left as far as we can. */ if (node->rb_right) { node = node->rb_right; while (node->rb_left) node=node->rb_left; return (struct rb_node *)node; } /* No right-hand children. Everything down and left is smaller than us, so any 'next' node must be in the general direction of our parent. Go up the tree; any time the ancestor is a right-hand child of its parent, keep going up. First time it's a left-hand child of its parent, said parent is our 'next' node. */ while ((parent = rb_parent(node)) && node == parent->rb_right) node = parent; return parent; } 六、在應(yīng)用程序中使用
Linux內(nèi)核中紅黑樹算法的實現(xiàn)非常通用、巧妙,而且免費又開源,因此完全可以把它運用到自己的應(yīng)用程序中。
(1)、從內(nèi)核中拷貝源文件:
$ mkdir redblack $ cd redblack/ $ cp ../linux-2.6.38.8/lib/rbtree.c . $ cp ../linux-2.6.38.8/include/linux/rbtree.h .
(2)、修改源文件:
a、C文件rbtree.c
修改包含頭文件的代碼
//刪除以下兩行代碼 #include <linux/rbtree.h> #include <linux/module.h> //新增以下代碼,即包含當前目錄中的頭文件rbtree.h #include "rbtree.h"
刪除所有的EXPORT_SYMBOL宏
EXPORT_SYMBOL(rb_insert_color); EXPORT_SYMBOL(rb_erase); EXPORT_SYMBOL(rb_augment_insert); EXPORT_SYMBOL(rb_augment_erase_begin); EXPORT_SYMBOL(rb_augment_erase_end); EXPORT_SYMBOL(rb_first); EXPORT_SYMBOL(rb_last); EXPORT_SYMBOL(rb_next); EXPORT_SYMBOL(rb_prev); EXPORT_SYMBOL(rb_replace_node);
b、頭文件rbtree.h
刪除包含頭文件的代碼,并添加三個宏定義
//刪除以下兩行代碼 #include <linux/kernel.h> #include <linux/stddef.h> /* linux-2.6.38.8/include/linux/stddef.h */ #undef NULL #if defined(__cplusplus) #define NULL 0 #else #define NULL ((void *)0) #endif /* linux-2.6.38.8/include/linux/stddef.h */ #define offsetof(TYPE, MEMBER) ((size_t) &((TYPE *)0)->MEMBER) /* linux-2.6.38.8/include/linux/kernel.h */ #define container_of(ptr, type, member) ({ / const typeof( ((type *)0)->member ) *__mptr = (ptr); / (type *)( (char *)__mptr - offsetof(type,member) );}) (3)、示例代碼
Linux內(nèi)核紅黑樹的使用方法請參考linux-2.6.38.8/Documentation/rbtree.txt文件。
/* test.c */ #include <stdio.h> #include <stdlib.h> #include "rbtree.h" struct mytype { struct rb_node my_node; int num; }; struct mytype *my_search(struct rb_root *root, int num) { struct rb_node *node = root->rb_node; while (node) { struct mytype *data = container_of(node, struct mytype, my_node); if (num < data->num) node = node->rb_left; else if (num > data->num) node = node->rb_right; else return data; } return NULL; } int my_insert(struct rb_root *root, struct mytype *data) { struct rb_node **tmp = &(root->rb_node), *parent = NULL; /* Figure out where to put new node */ while (*tmp) { struct mytype *this = container_of(*tmp, struct mytype, my_node); parent = *tmp; if (data->num < this->num) tmp = &((*tmp)->rb_left); else if (data->num > this->num) tmp = &((*tmp)->rb_right); else return -1; } /* Add new node and rebalance tree. */ rb_link_node(&data->my_node, parent, tmp); rb_insert_color(&data->my_node, root); return 0; } void my_delete(struct rb_root *root, int num) { struct mytype *data = my_search(root, num); if (!data) { fprintf(stderr, "Not found %d./n", num); return; } rb_erase(&data->my_node, root); free(data); } void print_rbtree(struct rb_root *tree) { struct rb_node *node; for (node = rb_first(tree); node; node = rb_next(node)) printf("%d ", rb_entry(node, struct mytype, my_node)->num); printf("/n"); } int main(int argc, char *argv[]) { struct rb_root mytree = RB_ROOT; int i, ret, num; struct mytype *tmp; if (argc < 2) { fprintf(stderr, "Usage: %s num/n", argv[0]); exit(-1); } num = atoi(argv[1]); printf("Please enter %d integers:/n", num); for (i = 0; i < num; i++) { tmp = malloc(sizeof(struct mytype)); if (!tmp) perror("Allocate dynamic memory"); scanf("%d", &tmp->num); ret = my_insert(&mytree, tmp); if (ret < 0) { fprintf(stderr, "The %d already exists./n", tmp->num); free(tmp); } } printf("/nthe first test/n"); print_rbtree(&mytree); my_delete(&mytree, 21); printf("/nthe second test/n"); print_rbtree(&mytree); return 0; } 編譯并執(zhí)行:
$ gcc rbtree.c test.c -o test richard@tanglinux:~/algorithm/redblack$ ./test 10 Please enter 10 integers: 23 4 56 32 89 122 12 21 45 23 The 23 already exists. the first test 4 12 21 23 32 45 56 89 122 the second test 4 12 23 32 45 56 89 122
七、總結(jié)
以上就是關(guān)于Linux內(nèi)核中紅黑樹算法實現(xiàn)的全部內(nèi)容,文章介紹的很詳細,希望對大家的工作和學(xué)習(xí)能有所幫助,如果有疑問可以留言交流。
新聞熱點
疑難解答