本文為大家分享了決策樹之C4.5算法，供大家參考，具體內(nèi)容如下

1. C4.5算法簡介

  C4.5算法是用于生成決策樹的一種經(jīng)典算法，是ID3算法的一種延伸和優(yōu)化。C4.5算法對ID3算法主要做了一下幾點改進：

  （1）通過信息增益率選擇分裂屬性，克服了ID3算法中通過信息增益傾向于選擇擁有多個屬性值的屬性作為分裂屬性的不足；
  （2）能夠處理離散型和連續(xù)型的屬性類型，即將連續(xù)型的屬性進行離散化處理；
  （3）構造決策樹之后進行剪枝操作；
  （4）能夠處理具有缺失屬性值的訓練數(shù)據(jù)。

2. 分裂屬性的選擇——信息增益率

  分裂屬性選擇的評判標準是決策樹算法之間的根本區(qū)別。區(qū)別于ID3算法通過信息增益選擇分裂屬性，C4.5算法通過信息增益率選擇分裂屬性。

  屬性A的“分裂信息”(split information)：

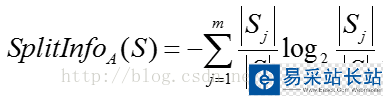
其中，訓練數(shù)據(jù)集S通過屬性A的屬性值劃分為m個子數(shù)據(jù)集，|Sj|表示第j個子數(shù)據(jù)集中樣本數(shù)量，|S|表示劃分之前數(shù)據(jù)集中樣本總數(shù)量。

  通過屬性A分裂之后樣本集的信息增益：

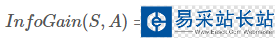
信息增益的詳細計算方法，可以參考博客“決策樹之ID3算法及其Python實現(xiàn)”中信息增益的計算。

  通過屬性A分裂之后樣本集的信息增益率：

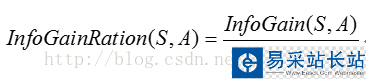
  通過C4.5算法構造決策樹時，信息增益率最大的屬性即為當前節(jié)點的分裂屬性，隨著遞歸計算，被計算的屬性的信息增益率會變得越來越小，到后期則選擇相對比較大的信息增益率的屬性作為分裂屬性。

3. 連續(xù)型屬性的離散化處理

  當屬性類型為離散型，無須對數(shù)據(jù)進行離散化處理；當屬性類型為連續(xù)型，則需要對數(shù)據(jù)進行離散化處理。C4.5算法針對連續(xù)屬性的離散化處理，核心思想：將屬性A的N個屬性值按照升序排列；通過二分法將屬性A的所有屬性值分成兩部分（共有N-1種劃分方法，二分的閾值為相鄰兩個屬性值的中間值）；計算每種劃分方法對應的信息增益，選取信息增益最大的劃分方法的閾值作為屬性A二分的閾值。詳細流程如下：
（1）將節(jié)點Node上的所有數(shù)據(jù)樣本按照連續(xù)型屬性A的具體取值，由小到大進行排列，得到屬性A的屬性值取值序列(xA1,...,xAN)。