前言
最小二乘法Least Square Method,做為分類回歸算法的基礎,有著悠久的歷史(由馬里·勒讓德于1806年提出)。它通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知的數據,并使得這些求得的數據與實際數據之間誤差的平方和為最小。最小二乘法還可用于曲線擬合。其他一些優化問題也可通過最小化能量或最大化熵用最小二乘法來表達。
下面這篇文章主要跟大家介紹了關于python中matplotlib實現最小二乘法擬合的相關內容,下面話不多說,來一起看看詳細的介紹:
一、最小二乘法擬合直線
生成樣本點
首先,我們在直線 y = 3 + 5x 附近生成服從正態分布的隨機點,作為擬合直線的樣本點。
import numpy as np import matplotlib.pyplot as plt# 在直線 y = 3 + 5x 附近生成隨機點X = np.arange(0, 5, 0.1) Z = [3 + 5 * x for x in X] Y = [np.random.normal(z, 0.5) for z in Z]plt.plot(X, Y, 'ro') plt.show()
樣本點如圖所示:
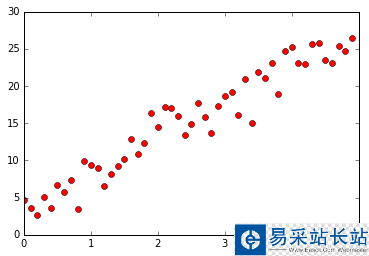
擬合直線
設 y = a0 + a1*x,我們利用最小二乘法的正則方程組來求解未知系數 a0 與 a1。
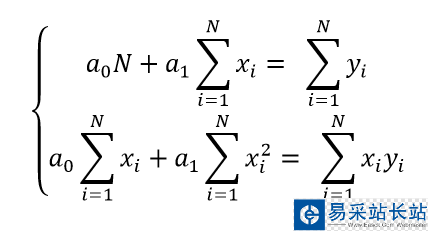
numpy 的 linalg 模塊中有一個 solve 函數,它可以根據方程組的系數矩陣和方程右端構成的向量來求解未知量。
def linear_regression(x, y): N = len(x) sumx = sum(x) sumy = sum(y) sumx2 = sum(x**2) sumxy = sum(x*y) A = np.mat([[N, sumx], [sumx, sumx2]]) b = np.array([sumy, sumxy]) return np.linalg.solve(A, b)a0, a1 = linear_regression(X, Y)
繪制直線
此時,我們已經得到了擬合后的直線方程系數 a0 和 a1。接下來,我們繪制出這條直線,并與樣本點做對比。
# 生成擬合直線的繪制點_X = [0, 5] _Y = [a0 + a1 * x for x in _X]plt.plot(X, Y, 'ro', _X, _Y, 'b', linewidth=2) plt.title("y = {} + {}x".format(a0, a1)) plt.show() 擬合效果如下:
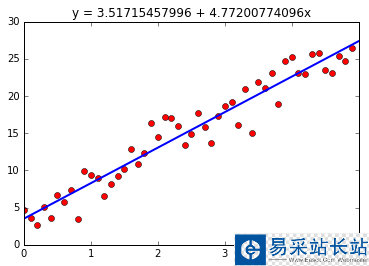
二、最小二乘法擬合曲線
生成樣本點
與生成直線樣本點相同,我們在曲線 y = 2 + 3x + 4x^2 附近生成服從正態分布的隨機點,作為擬合曲線的樣本點。
import numpy as np import matplotlib.pyplot as plt# y = 2 + 3x + 4x^2X = np.arange(0, 5, 0.1) Z = [2 + 3 * x + 4 * x ** 2 for x in X] Y = np.array([np.random.normal(z,3) for z in Z])plt.plot(X, Y, 'ro') plt.show()
樣本點如圖所示:
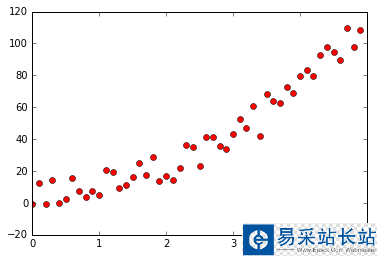
擬合曲線
設該曲線的方程為 y = a0 + a1*x + a2*x^2,同樣,我們通過正則方程組來求解未知量 a0、a1 和 a2。
新聞熱點
疑難解答