前言

之前一直寫不出來，這周周日花了一下午終于弄懂了， 順便放博客里，方便以后忘記了再看看。
要實現的是輸入一張 圖，起點，終點，輸出起點和終點之間的最短路徑。

廣度優先搜索

適用范圍： 無權重的圖，與深度優先搜索相比，深度優先搜索法占內存少但速度較慢，廣度優先搜索算法占內存多但速度較快

復雜度： 時間復雜度為O(V+E),V為頂點數，E為邊數

思路

廣度優先搜索是以層為順序,將某一層上的所有節點都搜索到了之后才向下一層搜索；
比如下圖：

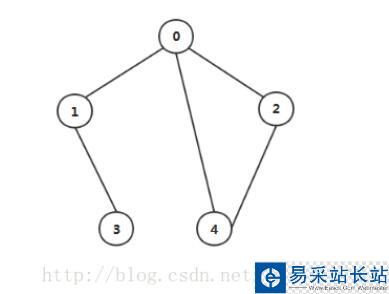
從0結點開始搜索的話，一開始是0、將0加入隊列中；
然后下一層，0可以到達的有1,2,4,將他們加入隊列中；
接下來是1，1能到達的且未被訪問的是結點3
順序就是 0， 1，2，4， 3，這里用下劃線表示每一層搜索得到的結點；

每一次用cur = que[head]取出頭指針指向的結點，并搜索它能到達的結點；因此，可以用一個隊列que來保存已經訪問過的結點,隊列有頭指針head以及尾指針tail,起點start與結點i有邊并且結點i未被訪問過，則將該結點加入隊列中,tail指針往后移動；當tail等于頂點數時算法結束

對于每一次while循環，head都加一，也就是往右邊移動，比如一開始head位置是0，下一層的時候head位置元素就為1，也就是搜索與結點1有邊的且未被訪問的結點

用一個數組book來標識結點i是否已經被訪問過；用字典來保存起點到各個點的最短路徑；
代碼如下：

import numpy as npini_matrix = [     [0, 1, 1, 0, 1],     [1, 0, 0, 1, 0],     [1, 0, 0, 0, 1],     [0, 1, 0, 0, 0],     [1, 0, 1, 0, 0]     ]def bfs(matrix_para, start_point_para, end_point_para):  """  廣度優先搜索  :param matrix_para 圖  :param start_point_para 起點  :param end_point_para 終點  :return: 返回關聯度  """  matrix = matrix_para  start_point = start_point_para  end_point = end_point_para  vertex_num = len(matrix) # 頂點個數  que = np.zeros(vertex_num, dtype=np.int) # 隊列， 用于存儲遍歷過的頂點  book = np.zeros(vertex_num, dtype=np.int) # 標記頂點i是否已經被訪問，1表被訪問，0表未被訪問  point_step_dict = dict() # key:點，value:起點到該點的步長  # 隊列初始化  head = 0  tail = 0  # 從起點出發，將起點加入隊列  que[tail] = start_point # 等號右邊為頂點號（起點）  tail += 1  book[start_point] = 1 # book[i] i為頂點號  while head<tail:    cur = que[head]    for i in range(vertex_num):      # 判斷從頂點cur到頂點i是否有邊，并判斷頂點i是否已經被訪問過      if matrix[cur][i] == 1 and book[i] == 0:        que[tail] = i # 將頂點i放入隊列中        tail += 1 # tail指針往后移        book[i] = 1 # 標記頂點i為已經訪問過        point_step_dict[i] = head + 1 # 記錄步長      if tail == vertex_num: # 說明所有頂點都被訪問過        break    head += 1  for i in range(tail):    print(que[i])  try:    relevancy = point_step_dict[end_point]    return relevancy  except KeyError: # 捕獲錯誤，如果起點不能到達end_point，則字典里沒有這個鍵，返回None    return Noneresult = bfs(ini_matrix, 1, 4)print("result:", result)