本文實(shí)例講述了Python使用numpy產(chǎn)生正態(tài)分布隨機(jī)數(shù)的向量或矩陣操作。分享給大家供大家參考，具體如下：

簡單來說，正態(tài)分布（Normal distribution）又名高斯分布（Gaussian distribution），是一個(gè)在數(shù)學(xué)、物理及工程等領(lǐng)域都非常重要的概率分布，在統(tǒng)計(jì)學(xué)的許多方面有著重大的影響力。一般的正態(tài)分布可以通過標(biāo)準(zhǔn)正態(tài)分布配合數(shù)學(xué)期望向量和協(xié)方差矩陣得到。如下代碼，可以得到滿足一維和二維正態(tài)分布的樣本。

示例1（一維正態(tài)分布）：

# coding=utf-8'''作者：采石工來源：知乎'''import numpy as npfrom numpy.linalg import choleskyimport matplotlib.pyplot as pltsampleNo = 1000;# 一維正態(tài)分布# 下面三種方式是等效的mu = 3sigma = 0.1np.random.seed(0)s = np.random.normal(mu, sigma, sampleNo )plt.subplot(141)plt.hist(s, 30, normed=True)np.random.seed(0)s = sigma * np.random.randn(sampleNo ) + muplt.subplot(142)plt.hist(s, 30, normed=True)np.random.seed(0)s = sigma * np.random.standard_normal(sampleNo ) + muplt.subplot(143)plt.hist(s, 30, normed=True)# 二維正態(tài)分布mu = np.array([[1, 5]])Sigma = np.array([[1, 0.5], [1.5, 3]])R = cholesky(Sigma)s = np.dot(np.random.randn(sampleNo, 2), R) + muplt.subplot(144)# 注意繪制的是散點(diǎn)圖，而不是直方圖plt.plot(s[:,0],s[:,1],'+')plt.show()

運(yùn)行結(jié)果：

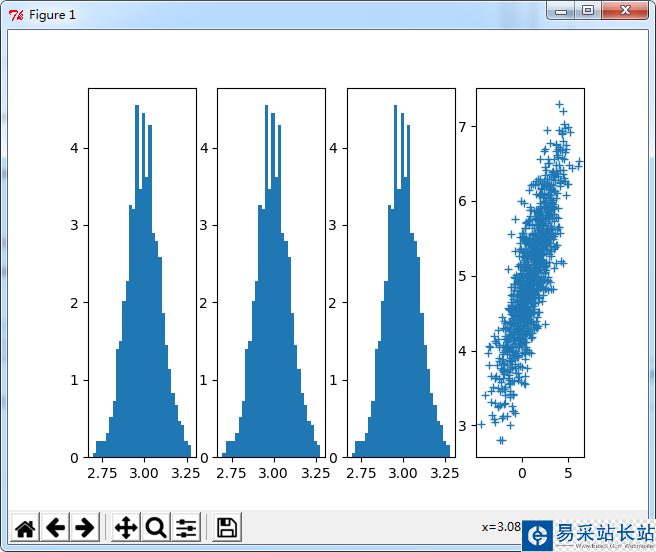
示例2（正態(tài)分布）：

#-*- coding:utf-8 -*-# Python實(shí)現(xiàn)正態(tài)分布# 繪制正態(tài)分布概率密度函數(shù)import numpy as npimport matplotlib.pyplot as pltimport mathu = 0  # 均值μu01 = -2sig = math.sqrt(0.2) # 標(biāo)準(zhǔn)差δx = np.linspace(u - 3*sig, u + 3*sig, 50)y_sig = np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig)print xprint "="*20print y_sigplt.plot(x, y_sig, "r-", linewidth=2)plt.grid(True)plt.show()

運(yùn)行結(jié)果：

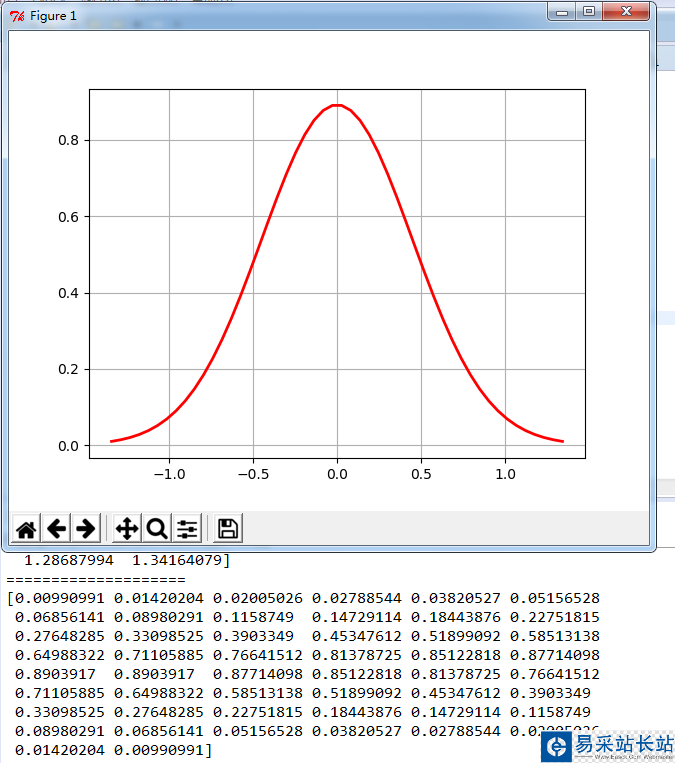
更多關(guān)于Python相關(guān)內(nèi)容感興趣的讀者可查看本站專題：《Python數(shù)據(jù)結(jié)構(gòu)與算法教程》、《Python編碼操作技巧總結(jié)》、《Python函數(shù)使用技巧總結(jié)》、《Python字符串操作技巧匯總》及《Python入門與進(jìn)階經(jīng)典教程》

希望本文所述對(duì)大家Python程序設(shè)計(jì)有所幫助。