Python基于回溯法子集樹模板實現(xiàn)圖的遍歷功能示例

2020-01-04 16:40:45

字體：大中小

來源：轉載

供稿：網(wǎng)友

本文實例講述了Python基于回溯法子集樹模板實現(xiàn)圖的遍歷功能。分享給大家供大家參考，具體如下：

問題

一個圖：

A --> B
A --> C
B --> C
B --> D
B --> E
C --> A
C --> D
D --> C
E --> F
F --> C
F --> D

從圖中的一個節(jié)點E出發(fā)，不重復地經(jīng)過所有其它節(jié)點后，回到出發(fā)節(jié)點E，稱為一條路徑。請找出所有可能的路徑。

分析

將這個圖可視化如下：

Python,回溯法,子集樹模板,圖的遍歷

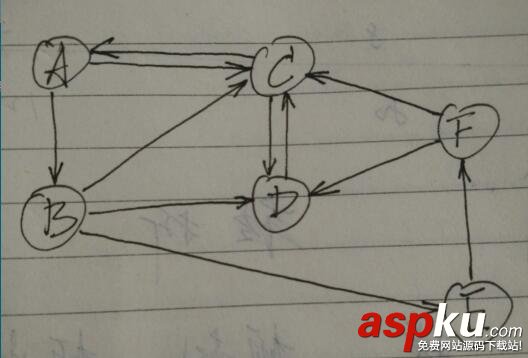
本問題涉及到圖，那首先要考慮圖用那種存儲結構表示。鄰接矩陣、鄰接表、...都不太熟。

接下來對問題本身進行分析：

顯然，問題的解的長度是固定的，亦即所有的路徑長度都是固定的：n（不回到出發(fā)節(jié)點）或 n+1（回到出發(fā)節(jié)點）

每個節(jié)點，都有各自的鄰接節(jié)點。

對某個節(jié)點來說，它的所有鄰接節(jié)點，可以看作這個節(jié)點的狀態(tài)空間。遍歷其狀態(tài)空間，剪枝，深度優(yōu)先遞歸到下一個節(jié)點。搞定！

至此，很明顯套用回溯法子集樹模板。

代碼：

'''圖的遍歷從一個節(jié)點出發(fā)，不重復地經(jīng)過所有其它節(jié)點后，回到出發(fā)節(jié)點。找出所有的路徑'''# 用鄰接表表示圖n = 6 # 節(jié)點數(shù)a,b,c,d,e,f = range(n) # 節(jié)點名稱graph = [  {b,c},  {c,d,e},  {a,d},  {c},  {f},  {c,d}]x = [0]*(n+1) # 一個解（n+1元數(shù)組，長度固定）X = []     # 一組解# 沖突檢測def conflict(k):  global n,graph,x  # 第k個節(jié)點，是否前面已經(jīng)走過  if k < n and x[k] in x[:k]:    return True  # 回到出發(fā)節(jié)點  if k == n and x[k] != x[0]:    return True  return False # 無沖突# 圖的遍歷def dfs(k): # 到達（解x的）第k個節(jié)點  global n,a,b,c,d,e,f,graph,x,X  if k > n: # 解的長度超出，已走遍n+1個節(jié)點 （若不回到出發(fā)節(jié)點，則 k==n）    print(x)    #X.append(x[:])  else:    for node in graph[x[k-1]]: # 遍歷節(jié)點x[k]的鄰接節(jié)點（x[k]的所有狀態(tài)）      x[k] = node      if not conflict(k): # 剪枝        dfs(k+1)# 測試x[0] = e # 出發(fā)節(jié)點dfs(1)  # 開始處理解x中的第2個節(jié)點

效果圖：

Python,回溯法,子集樹模板,圖的遍歷