聚類
今天說K-meanspython/78037.html">聚類算法,但是必須要先理解聚類和分類的區別,很多業務人員在日常分析時候不是很嚴謹,混為一談,其實二者有本質的區別。
分類其實是從特定的數據中挖掘模式,作出判斷的過程。比如Gmail郵箱里有垃圾郵件分類器,一開始的時候可能什么都不過濾,在日常使用過程中,我人工對于每一封郵件點選“垃圾”或“不是垃圾”,過一段時間,Gmail就體現出一定的智能,能夠自動過濾掉一些垃圾郵件了。這是因為在點選的過程中,其實是給每一條郵件打了一個“標簽”,這個標簽只有兩個值,要么是“垃圾”,要么“不是垃圾”,Gmail就會不斷研究哪些特點的郵件是垃圾,哪些特點的不是垃圾,形成一些判別的模式,這樣當一封信的郵件到來,就可以自動把郵件分到“垃圾”和“不是垃圾”這兩個我們人工設定的分類的其中一個。
聚類的的目的也是把數據分類,但是事先我是不知道如何去分的,完全是算法自己來判斷各條數據之間的相似性,相似的就放在一起。在聚類的結論出來之前,我完全不知道每一類有什么特點,一定要根據聚類的結果通過人的經驗來分析,看看聚成的這一類大概有什么特點。
1、概述
k-means是一種非常常見的聚類算法,在處理聚類任務中經常使用。K-means算法是集簡單和經典于一身的基于距離的聚類算法
采用距離作為相似性的評價指標,即認為兩個對象的距離越近,其相似度就越大。
該算法認為類簇是由距離靠近的對象組成的,因此把得到緊湊且獨立的簇作為最終目標。
2、核心思想
通過迭代尋找k個類簇的一種劃分方案,使得用這k個類簇的均值來代表相應各類樣本時所得的總體誤差最小。
k個聚類具有以下特點:各聚類本身盡可能的緊湊,而各聚類之間盡可能的分開。
k-means算法的基礎是最小誤差平方和準則,
其代價函數是:
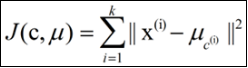
式中,μc(i)表示第i個聚類的均值。
各類簇內的樣本越相似,其與該類均值間的誤差平方越小,對所有類所得到的誤差平方求和,即可驗證分為k類時,各聚類是否是最優的。
上式的代價函數無法用解析的方法最小化,只能有迭代的方法。
3、算法步驟圖解
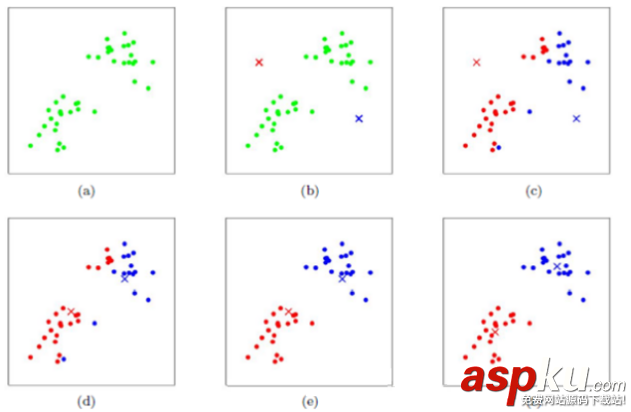
下圖展示了對n個樣本點進行K-means聚類的效果,這里k取2。
4、算法實現步驟
k-means算法是將樣本聚類成 k個簇(cluster),其中k是用戶給定的,其求解過程非常直觀簡單,具體算法描述如下:
1)隨機選取 k個聚類質心點
2)重復下面過程直到收斂 {
對于每一個樣例 i,計算其應該屬于的類:

對于每一個類 j,重新計算該類的質心:
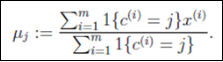
}
其偽代碼如下:
******************************************************************************
創建k個點作為初始的質心點(隨機選擇)
當任意一個點的簇分配結果發生改變時
對數據集中的每一個數據點
對每一個質心
計算質心與數據點的距離
將數據點分配到距離最近的簇
對每一個簇,計算簇中所有點的均值,并將均值作為質心
********************************************************
5、K-means聚類算法python實戰
需求:
對給定的數據集進行聚類
本案例采用二維數據集,共80個樣本,有4個類。

#!/usr/bin/python# coding=utf-8from numpy import *# 加載數據def loadDataSet(fileName): # 解析文件,按tab分割字段,得到一個浮點數字類型的矩陣 dataMat = [] # 文件的最后一個字段是類別標簽 fr = open(fileName) for line in fr.readlines(): curLine = line.strip().split('/t') fltLine = map(float, curLine) # 將每個元素轉成float類型 dataMat.append(fltLine) return dataMat# 計算歐幾里得距離def distEclud(vecA, vecB): return sqrt(sum(power(vecA - vecB, 2))) # 求兩個向量之間的距離# 構建聚簇中心,取k個(此例中為4)隨機質心def randCent(dataSet, k): n = shape(dataSet)[1] centroids = mat(zeros((k,n))) # 每個質心有n個坐標值,總共要k個質心 for j in range(n): minJ = min(dataSet[:,j]) maxJ = max(dataSet[:,j]) rangeJ = float(maxJ - minJ) centroids[:,j] = minJ + rangeJ * random.rand(k, 1) return centroids# k-means 聚類算法def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent): m = shape(dataSet)[0] clusterAssment = mat(zeros((m,2))) # 用于存放該樣本屬于哪類及質心距離 # clusterAssment第一列存放該數據所屬的中心點,第二列是該數據到中心點的距離 centroids = createCent(dataSet, k) clusterChanged = True # 用來判斷聚類是否已經收斂 while clusterChanged: clusterChanged = False; for i in range(m): # 把每一個數據點劃分到離它最近的中心點 minDist = inf; minIndex = -1; for j in range(k): distJI = distMeans(centroids[j,:], dataSet[i,:]) if distJI < minDist: minDist = distJI; minIndex = j # 如果第i個數據點到第j個中心點更近,則將i歸屬為j if clusterAssment[i,0] != minIndex: clusterChanged = True; # 如果分配發生變化,則需要繼續迭代 clusterAssment[i,:] = minIndex,minDist**2 # 并將第i個數據點的分配情況存入字典 print centroids for cent in range(k): # 重新計算中心點 ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]] # 去第一列等于cent的所有列 centroids[cent,:] = mean(ptsInClust, axis = 0) # 算出這些數據的中心點 return centroids, clusterAssment# --------------------測試----------------------------------------------------# 用測試數據及測試kmeans算法datMat = mat(loadDataSet('testSet.txt'))myCentroids,clustAssing = kMeans(datMat,4)print myCentroidsprint clustAssing運行結果:
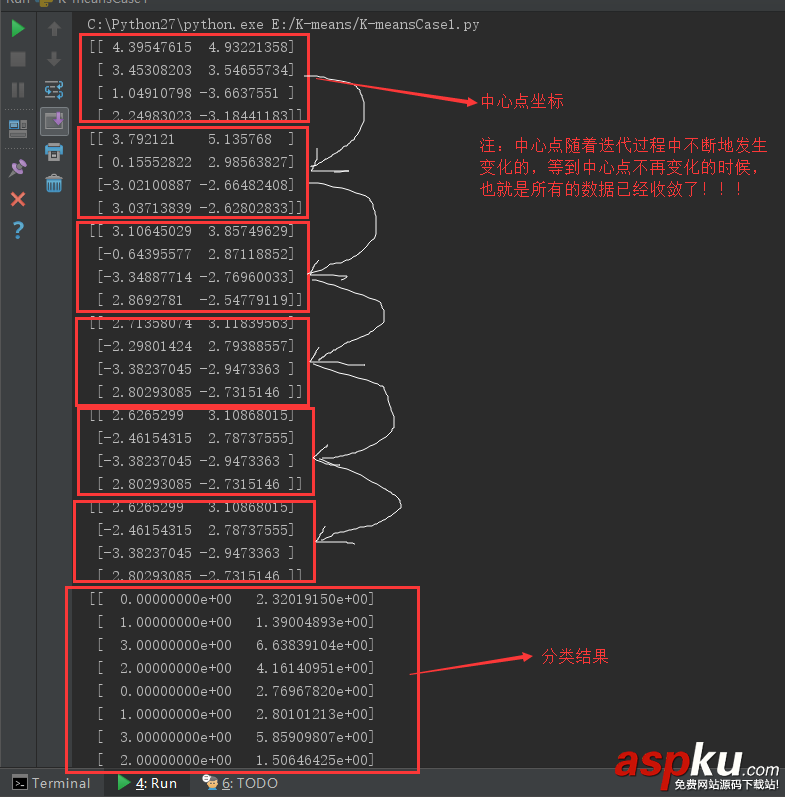
6、K-means算法補充
K-means算法的缺點及改進方法
(1)k值的選擇是用戶指定的,不同的k得到的結果會有挺大的不同,如下圖所示,左邊是k=3的結果,這個就太稀疏了,藍色的那個簇其實是可以再劃分成兩個簇的。而右圖是k=5的結果,可以看到紅色菱形和藍色菱形這兩個簇應該是可以合并成一個簇的:
改進:
對k的選擇可以先用一些算法分析數據的分布,如重心和密度等,然后選擇合適的k
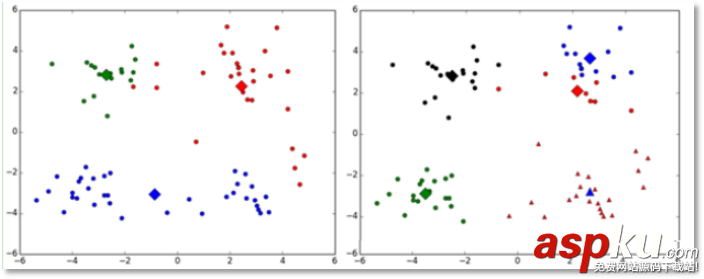
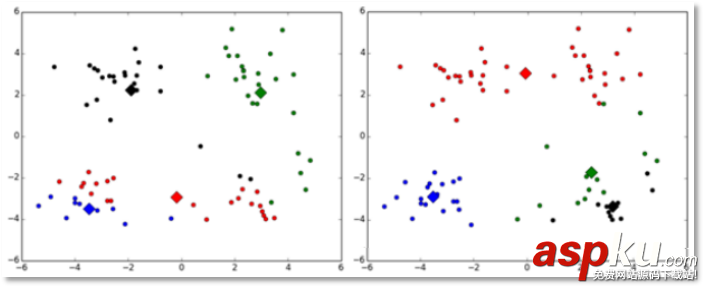
(2)對k個初始質心的選擇比較敏感,容易陷入局部最小值。例如,我們上面的算法運行的時候,有可能會得到不同的結果,如下面這兩種情況。K-means也是收斂了,只是收斂到了局部最小值:
改進:
有人提出了另一個成為二分k均值(bisecting k-means)算法,它對初始的k個質心的選擇就不太敏感
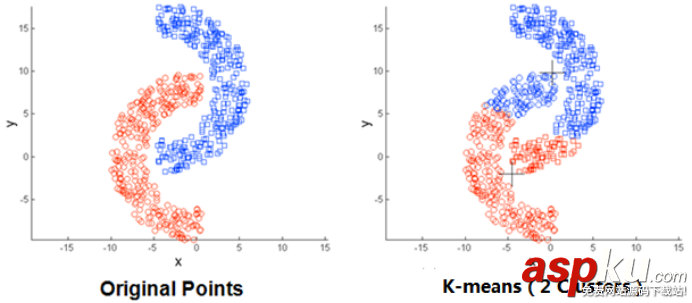
(3)存在局限性,如下面這種非球狀的數據分布就搞不定了:
(4)數據集比較大的時候,收斂會比較慢。
總結
以上就是這篇文章的全部內容了,希望本文的內容對大家的學習或者工作具有一定的參考學習價值,如果有疑問大家可以留言交流,謝謝大家對VEVB武林網的支持。
新聞熱點
疑難解答