本文實例講述了Python基于輾轉相除法求解最大公約數的方法。分享給大家供大家參考,具體如下:
之前總結過一次高德納TAOCP中的最大公約數求解,其實課后題中的算法修改要求實現的是輾轉相除法求解最大公約數。
這個題目我最初的理解理解錯了,自然也沒有做出標準答案。現在按照標準答案的解答寫一下相應的代碼實現:
# -*- coding:utf-8 -*-#! python2def MaxCommDivisor(m,n): while m * n != 0: m = m % n if m == 0: return n else: n = n % m if n == 0: return mprint(MaxCommDivisor(55,120))
程序的執行結果:
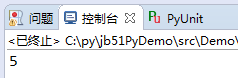
交換一下兩個數字的位置,代碼如下:
# -*- coding:utf-8 -*-#! python2def MaxCommDivisor(m,n): while m * n != 0: m = m % n if m == 0: return n else: n = n % m if n == 0: return mprint(MaxCommDivisor(120,55))
程序的執行結果:
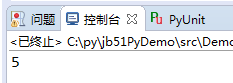
題目提示中提到了會降低效率,通過上面的代碼來看,效率的損失應該是在除法以及判斷上。在此,把之前算法的代碼拿過來對比一下:
def CommDevisor(m,n): r = m % n while r != 0: m = n n = r r = m % n return nprint(CommDevisor(120,25))
運行結果:
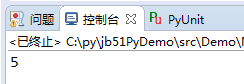
新算法在循環中,多了一個除法以及比較操作。其實,比較的效率還是不錯的,但是除法的運算會導致效率的降低。
希望本文所述對大家Python程序設計有所幫助。
新聞熱點
疑難解答