在神經網絡模型優化的過程中,會遇到許多問題,比如如何設置學習率的問題,我們可通過指數衰減的方式讓模型在訓練初期快速接近較優解,在訓練后期穩定進入最優解區域;針對過擬合問題,通過正則化的方法加以應對;滑動平均模型可以讓最終得到的模型在未知數據上表現的更加健壯。
一、學習率的設置
學習率設置既不能過大,也不能過小。TensorFlow提供了一種更加靈活的學習率設置方法——指數衰減法。該方法實現了指數衰減學習率,先使用較大的學習率來快速得到一個比較優的解,然后隨著迭代的繼續逐步減小學習率,使得模型在訓練后期更加穩定,緩慢平滑得達到最優值。
tf.train.exponential_decay(learning_rate, global_step, decay_steps, decay_rate,staircase=False, name=None)
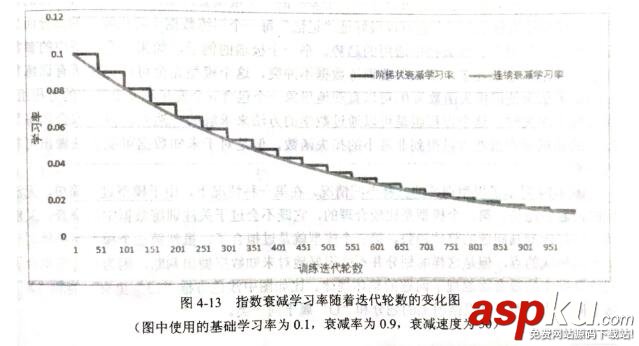
該函數會指數級減小學習率,實現每輪實際優化時的衰減后的學習率decayed_learning_rate = learning_rate * decay_rate ^ (global_step /decay_steps),learning_rate為設定的出事學習率,decay_rate為衰減系數,decay_steps為衰減速度。如下圖,參數staircase=False時,學習率變化趨勢為淺色部分;staircase=True時為深色部分,使得學習率變化為階梯函數(staircase function),這種設置的常用應用場景是每完整地過完一遍訓練數據,學習率就減小一次。
使用示例:learning_rate =tf.train.exponential_decay(starter_learning_rate, global_step, 100000, 0.96,staircase=True)。
二、過擬合問題
1. 過擬合問題及其解決方法
所謂過擬合問題,指的是當一個模型過于復雜后,它可以很好地記憶每一個訓練數據中隨機噪聲的部分而忘記了要去學習訓練數據中通用的趨勢。
為了避免過擬合問題,常用的方法是正則化(Regularization),思想是在損失函數中加入刻畫模型復雜程度的指標,將優化目標定義為J(θ)+λR(w) ,其中R(w)刻畫的是模型的復雜程度,包括了權重項w不包括偏置項b,λ表示模型復雜損失在總損失中的比例。一般來說模型復雜度只由權重w決定。常用的刻畫模型復雜度的函數R(w)有兩種,一種是L1正則化:
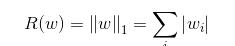
另一種是L2正則化:
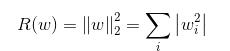
無論哪種正則化方式,基本思想都是希望通過限制權重的大小,使得模型不能任意擬合訓練數據中的隨機噪音。區別:L1正則化會讓參數變得更稀疏,L2則不會,所謂參數變得更稀疏是指會有更多的參數變為0,可達到類似特征選取的功能。實踐中,也可以將L1正則化和L2正則化同時使用:

2. 過擬合問題的TensorFlow解決方案
loss =tf.reduce_mean(tf.square(y_ - y) + tf.contrib.layers.l2_regularizer(lambda)(w)
以上就是一個含L2正則化項的損失函數。第一部分是均方誤差損失函數,第二部分就是正則化項。lambda參數表示正則化項的權重,也就是J(θ)+λR(w)中的λ,w為需要計算正則化損失的參數。tf.contrib.layers.l2_regularize()函數可以計算給定參數的L2正則化項,類似地,tf.contrib.layers.l1_regularizer()可以就是那給定參數的L1正則化項。
# 比較L1正則化和L2正則化函數的作用效果 w = tf.constant([[1.0, -2.0], [-3.0, 4.0]]) with tf.Session() as sess: # 0.5*(|1|+|-2|+|-3|+|4|=5.0) print(sess.run(tf.contrib.layers.l1_regularizer(0.5)(w))) # 5.0 # 0.5*[(1+4+9+16)/2]=7.5 TensorFlow會將L2正則化項除以2使得求導的結果更簡潔 print(sess.run(tf.contrib.layers.l2_regularizer(0.5)(w))) # 7.5
當神經網絡的參數增多以后,上面的定義損失函數的方式會導致loss的定義式很長,可讀性差,另外當網絡結構復雜后定義網絡結構的部分和計算損失函數的部分可能不在同一個函數中,通過變量方式計算損失函數就不方便了。為解決此問題,可以使用TensorFlow中提供的集合(collection)。具體實現見代碼部分。
tf.add_to_collection()將變量加入至指定集合中;tf.get_collection()返回一個列表,存儲著這個集合中的元素。
三、滑動平均模型
另一個使模型在測試數據上更健壯(robust)滑動平均模型。在采用隨機梯度下降算法訓練神經網絡時,使用滑動平均模型在很多應用中可提高最終模型在測試數據上的表現,GradientDescent和Momentum方式的訓練都能夠從ExponentialMovingAverage方法中獲益。
在TensorFlow中提供的tf.train.ExponentialMovingAverage是一個類class,來實現滑動平均模型。初始化tf.train.ExponentialMovingAverage類對象時,須指定衰減率decay和用于動態控制衰減率的參數num_updates。tf.train.ExponentialMovingAverage對每一個變量維護一個影子變量(shadow variable),該影子變量的初始值就是相應變量的初始值,每次變量更新時,shadow_variable =decay * shadow_variable + (1 - decay) * variable。從公式中可看出,decay決定了模型更新的速度,decay越大模型越趨于穩定,實際應用中decay一般設置為接近1的數。num_updates默認是None,若設置了,則衰減率按min(decay, (1 +num_updates) / (10 + num_updates))計算。
tf.train.ExponentialMovingAverage對象的apply方法返回一個對var_list進行更新滑動平均的操作,var_list必須是list的Variable或Tensor,該操作執行會更新var_list的影子變量shadowvariable。average方法可獲取滑動平均后變量的取值。
四、代碼呈現
1. 復雜神經網絡結構權重L2正則化方法
import tensorflow as tf ''''' # 比較L1正則化和L2正則化函數的作用效果 w = tf.constant([[1.0, -2.0], [-3.0, 4.0]]) with tf.Session() as sess: # 0.5*(|1|+|-2|+|-3|+|4|=5.0) print(sess.run(tf.contrib.layers.l1_regularizer(0.5)(w))) # 5.0 # 0.5*[(1+4+9+16)/2]=7.5 TensorFlow會將L2正則化項除以2使得求導的結果更簡潔 print(sess.run(tf.contrib.layers.l2_regularizer(0.5)(w))) # 7.5 ''' # 復雜神經網絡結構權重L2正則化方法 # 定義各層的權重,并將該權重的L2正則化項加入至名稱為‘losses'的集合 def get_weight(shape, lambda1): var = tf.Variable(tf.random_normal(shape), dtype=tf.float32) tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var)) return var x = tf.placeholder(tf.float32, (None, 2)) y_ = tf.placeholder(tf.float32, (None, 1)) layer_dimension = [2,10,5,3,1] # 定義了神經網絡每層的節點數 n_layers = len(layer_dimension) current_layer = x # 將當前層設置為輸入層 in_dimension = layer_dimension[0] # 通過循環生成一個5層全連接的神經網絡結構 for i in range(1,n_layers): out_dimension = layer_dimension[i] weight = get_weight([in_dimension,out_dimension], 0.003) bias = tf.Variable(tf.constant(0.1, shape=[out_dimension])) current_layer = tf.nn.relu(tf.matmul(current_layer, weight) + bias) in_dimension = layer_dimension[i] mse_loss = tf.reduce_mean(tf.square(y_ - current_layer)) tf.add_to_collection('losses', mse_loss) loss = tf.add_n(tf.get_collection('losses')) # 包含所有參數正則化項的損失函數 2. tf.train.ExponentialMovingAverage使用樣例
import tensorflow as tf # tf.train.ExponentialMovingAverage使用樣例 v1 = tf.Variable(0, dtype=tf.float32) step = tf.Variable(0, trainable=False) # 此處step模擬神經網絡迭代的輪數 # 定義一個滑動平均的類對象,初始化衰減率decay=0.99,用于動態控制衰減率的參數num_updates ema = tf.train.ExponentialMovingAverage(0.99, num_updates=step) # apply方法返回一個對var_list進行更新滑動平均的操作,var_list必須是list的Variable或Tensor # 該操作執行會更新var_list的影子變量shadow variable maintain_averages_op = ema.apply(var_list=[v1]) with tf.Session() as sess: init_op = tf.global_variables_initializer() sess.run(init_op) # average方法可獲取滑動平均后變量的取值 print(sess.run([v1, ema.average(v1)])) # [0.0, 0.0] sess.run(tf.assign(v1, 5)) # min{0.99, (1+step)(10+step)=0.1}=0.1 # 更新v1的滑動平均值為 0.1*0.0+0.9*5=4.5 sess.run(maintain_averages_op) print(sess.run([v1, ema.average(v1)])) # [5.0, 4.5] sess.run(tf.assign(step, 10000)) sess.run(tf.assign(v1, 10)) # min{0.99, (1+step)(10+step)=0.999}=0.99 # 更新v1的滑動平均值為 0.99*4.5+0.01*10=4.555 sess.run(maintain_averages_op) print(sess.run([v1, ema.average(v1)])) # [10.0, 4.5549998] # 更新v1的滑動平均值為 0.99*4.555+0.01*10=4.60945 sess.run(maintain_averages_op) print(sess.run([v1, ema.average(v1)])) # [10.0, 4.6094499] 以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持VEVB武林網。
新聞熱點
疑難解答