什么是遞歸函數/方法?
任何一個方法既可以調用其他方法也可以調用自己,而當這個方法調用自己時,我們就叫它遞歸函數或遞歸方法。
通常遞歸有兩個特點:
1. 遞歸方法一直會調用自己直到某些條件被滿足
2. 遞歸方法會有一些參數,而它會把一些新的參數值傳遞給自己。
那什么是遞歸函數?函數和方法沒有本質區別,但函數僅在類的內部使用。以前C#中只有方法,從.NET 3.5開始才有了匿名函數。
所以,我們最好叫遞歸方法,而非遞歸函數,本文中將統一稱之為遞歸。
在應用程序中為什么要使用遞歸?何時使用遞歸?如何用?
“寫任何一個程序可以用賦值和if-then-else語句表示出來,而while語句則可以用賦值、if-then-else和遞歸表示出來。”(出自Ellis Horowitz的《數據結構基礎(C語言版)》 - Fundamentals of Data Structure in C)
遞歸解決方案對于復雜的開發來說很方便,而且十分強大,但由于頻繁使用調用棧(call stack)可能會引起性能問題(有些時候性能極差)。
我們來看一看下面這個圖:
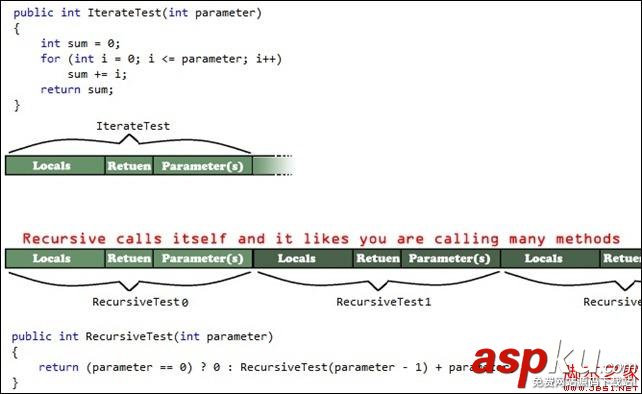
調用棧圖示
下面我打算介紹一些例子來幫助你更好的理解遞歸的風險和回報。
1. 階乘
階乘(!)是小于某個數的所有正整數的乘積。
0! = 1
1! = 1
2! = 2 * 1! = 2
3! = 3 * 2! = 6
...
n! = n * (n - 1)!
下面是計算階乘的一種實現方法(沒有遞歸):
復制代碼代碼如下:
public long Factorial(int n)
{
if (n == 0)
return 1;
long value = 1;
for (int i = n; i > 0; i--)
{
value *= i;
}
return value;
}
下面是用遞歸的方法實現計算階乘,與之前的代碼比起來它更簡潔。
復制代碼代碼如下:
public long Factorial(int n)
{
if (n == 0)//限制條件,對該方法調用自己做了限制
return 1;
return n * Factorial(n - 1);
}
你知道的,n的階乘實際上是n-1的階乘乘以n,且n>0。
它可以表示成 Factorial(n) = Factorial(n-1) * n
這是方法的返回值,但我們需要一個條件
如果 n=0 返回1。
現在這個程式的邏輯應該很清楚了,這樣我們就能夠輕易的理解。
2. Fibonacci數列
Fibonacci數列是按以下順序排列的數字:
0,1,1,2,3,5,8,13,21,34,55,…如果F0 = 0 并且 F1= 1 那么Fn = Fn-1 + Fn-2
下面的方法就是用來計算Fn的(沒有遞歸,性能好)
復制代碼代碼如下:
public long Fib(int n)
{
if (n < 2)
return n;
long[] f = new long[n+1];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
如果我們使用遞歸方法,這個代碼將更加簡單,但性能很差。
復制代碼代碼如下:
public long Fib(int n)
{
if (n == 0 || n == 1) //滿足條件
return n;
return Fib(k - 2) + Fib(k - 1);
}
<STRONG><SPAN style="FONT-SIZE: medium">3. 布爾組合</SPAN></STRONG>
有時我們需要解決的問題比Fibonacci數列復雜很多,例如我們要枚舉所有的布爾變量的組合。換句話說,如果n=3,那么我們必須輸出如下結果:
true, true, true
true, true, false
true, false, true
true, false, false
false, true, true
false, true, false
false, false, true
false, false, false如果n很大,且不用遞歸是很難解決這個問題的。
復制代碼代碼如下:
public void CompositionBooleans(string result, int counter)
{
if (counter == 0)
return;
bool[] booleans = new bool[2] { true, false };
for (int j = 0; j < 2; j++)
{
StringBuilder stringBuilder = new StringBuilder(result);
stringBuilder.Append(string.Format("{0} ", booleans[j].ToString())).ToString();
if (counter == 1)
Console.WriteLine(stringBuilder.ToString());
CompositionBooleans(stringBuilder.ToString(), counter - 1);
}
}
現在讓我們來調用上面這個方法:
復制代碼代碼如下:
CompositionBoolean(string.Empty, 3);
Ian Shlasko建議我們這樣使用遞歸:
復制代碼代碼如下:
public void BooleanCompositions(int count)
{
BooleanCompositions(count - 1, "true");
BooleanCompositions(count - 1, "false");
}
private void BooleanCompositions(int counter, string partialOutput)
{
if (counter <= 0)
Console.WriteLine(partialOutput);
else
{
BooleanCompositions(counter - 1, partialOutput+ ", true");
BooleanCompositions(counter - 1, partialOutput+ ", false");
}
}
4. 獲取內部異常
如果你想獲得innerException,那就選擇遞歸方法吧,它很有用。
復制代碼代碼如下:
public Exception GetInnerException(Exception ex)
{
return (ex.InnerException == null) ? ex : GetInnerException(ex.InnerException);
}
為什么要獲得最后一個innerException呢?!這不是本文的主題,我們的主題是如果你想獲得最里面的innerException,你可以靠遞歸方法來完成。
這里的代碼:
復制代碼代碼如下:
return (ex.InnerException == null) ? ex : GetInnerException(ex.InnerException);
與下面的代碼等價
復制代碼代碼如下:
if (ex.InnerException == null)//限制條件
return ex;
return GetInnerException(ex.InnerException);//用內部異常作為參數調用自己
現在,一旦我們獲得了一個異常,我們就能找到最里面的innerException。例如:
復制代碼代碼如下:
try
{
throw new Exception("This is the exception",
new Exception("This is the first inner exception.",
new Exception("This is the last inner exception.")));
}
catch (Exception ex)
{
Console.WriteLine(GetInnerException(ex).Message);
}
我曾經想寫關于匿名遞歸方法的文章,但是我發覺我的解釋無法超越那篇文章。
5. 查找文件
我在供你下載的示范項目中使用了遞歸,通過這個項目你可以搜索某個路徑,并獲得當前文件夾和其子文件夾中所有文件的路徑。
復制代碼代碼如下:
private Dictionary<string, string> errors = new Dictionary<string, string>();
private List<string> result = new List<string>();
private void SearchForFiles(string path)
{
try
{
foreach (string fileName in Directory.GetFiles(path))//Gets all files in the current path
{
result.Add(fileName);
}
foreach (string directory in Directory.GetDirectories(path))//Gets all folders in the current path
{
SearchForFiles(directory);//The methods calls itself with a new parameter, here!
}
}
catch (System.Exception ex)
{
errors.Add(path, ex.Message);//Stores Error Messages in a dictionary with path in key
}
}
這個方法似乎不需要滿足任何條件,因為每個目錄如果沒有子目錄,會自動遍歷所有子文件。
總結
我們其實可以用遞推算法來替代遞歸,且性能會更好些,但我們可能需要更多的時間開銷和非遞歸函數。但關鍵是我們必須根據場景選擇最佳實現方式。
James MaCaffrey博士認為盡量不要使用遞歸,除非實在沒有辦法。你可以讀一下他的文章。
我認為:
A) 如果性能是非常重要的,請避免使用遞歸
B)如果遞推方式不是很復雜的,請避免使用遞歸
C) 如果A和B都不滿足,請不要猶豫,用遞歸吧。
例如:
第一節(階乘):這里用遞推并不復雜,那么就避免用遞歸。
第二節(Fibonacci):像這樣的遞歸并不被推薦。
當然,我并不是要貶低遞歸的價值,我記得人工智能中的重要一章有個極小化極大算法(Minimax algorithm),全部是用遞歸實現的。
但是如果你決定使用隊規方法,你最好嘗試用存儲來優化它。
版權聲明:本文由作者Tony Qu原創, 未經作者同意必須保留此段聲明,且在文章頁面明顯位置給出原文連接,否則視為侵權。